高中数学联合竞赛模拟试题三
| 高中数学联合竞赛模拟试题三 |
|
第一试 一、选择题(每小题6分,共计36分) 1.定义在(-,-2)(2,+)上的函数f(x)= A.是奇函数不是偶函数 B.是偶函数不是奇函数 C.既是奇函数又是偶函数 D.既不是奇函数又不是偶函数 2.把直线l沿y轴平移sin-cos0)个单位,再沿x轴平移
A.不存在 B. 3.从正方体的8个顶点中取出3个,使至少有两个顶点在同一条棱上,其取法数为 A.44 B.48 C.50 D.52 4.对于函数f(x)= A. B.R C.单元素集合 D.二元素集合 5.设递增正数列a1,a2,,an是分母为60的最简真分数,则 A.0 B.8 C.16 D.30 6.存在x1,x2,,xn满足x A.2|n B.4|n C.6|n D.8|n 二、填空题(每小题9分,共计54分) 1.给定递推数列 2.在平面上有一个△ABC,ABC=105,AC=2( 3.过双曲线x2- 4.已知函数f(x)、g(x)在R上有定义,且f(x-y)=f(x)g(y)-g(x)f(y),若f⑴=f⑵0,则g⑴+g(-1)=___________________. 5.正实数x,y,z满足 6.一副桥牌有52张牌,将其排成一横行,任意两张A都不相邻的排列数为____________. 三、(20分)将一个1016的矩形铁皮,从四个角上各建取一个边长为x的正方形(0<x<5),然后做成一个无盖的长方体容器. ⑴写出容器的容积y与x的函数关系式; ⑵求y的最大值,并求相应的x的值. 四、(20分)对于、[0,2),记x=sin+sin,y=cos+cos,求直角坐标系上点(x,y)的轨迹. 五、(20分)求证:对于任给的正数a,必存在一个自然数N,使每一个大于N的自然数n都有惟一的自然数f(n),满足 第二试
二、(50分)设有两组正数:0<x1x2x3xn<1,0<y1y2y3yn,
求证: 三、(50分)设Sn={1,2,,n}(n5),取X |
- 吉林艺术学院2017招生章程
- 青岛大学2017年本科招生计划共8375人 省内招6374人
- 沈阳工业大学2017年招生计划5216人 在辽宁招2689人
- 西安美术学院2017年本科招生章程
- 吉林建筑大学城建学院2017招生章程
- 西安体育学院2017年招生章程
- 2017年吉林高考报名人数142940人
- 通化师范学院2017招生章程
- 国防部:2017年起不再从高中毕业生中定向招收国防生
- 东北电力大学2017招生章程
- 吉林警察学院2017招生章程
- 7月1日施行 学校招收和培养国际学生有新规
- 东北大学2017年新增机器人工程专业
- 沈阳药科大学2017年辽宁计划招生714人 比去年增加5人
- 苏州幼儿师范高等专科学校2017年招生章程
- 再见了国防生!国防生正式退出历史舞台
- 山东大学:“三跨四经历”提供更多国外学习机会
- :当前要特别警惕鼓吹应试教育的言论
- 中国医科大学2017年招生计划1993人 在辽宁招1068人
- 吉林师范大学2017招生章程
- 延边大学2017招生章程
- 西安理工大学2017年本科招生章程
- 榆林学院2017年普通高考招生章程
- 沈阳理工大学2017年辽宁计划招生2195人
- 长春师范大学2017招生章程
- 2017年所有高校国防生暂停招生
- 西安外国语大学2017年招生章程
- 山东职业学院2017年招生章程
- 长春财经学院2017招生章程
- 上海海关学院2017年招生章程
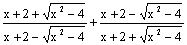 的奇偶性为
的奇偶性为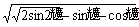 (>0)个单位,所得直线与原直线重合,则原直线的斜率为
(>0)个单位,所得直线与原直线重合,则原直线的斜率为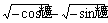 C.
C.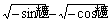 D.
D.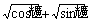
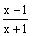 ,记f2(x)=f(f(x)),f3=f(f2(x)),,fn(x)=f(fn-1(x)),又记M为f1998(x)=x实根的解集,则M为
,记f2(x)=f(f(x)),f3=f(f2(x)),,fn(x)=f(fn-1(x)),又记M为f1998(x)=x实根的解集,则M为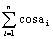 =
=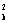 +1=0,且使
+1=0,且使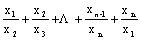 =0成立的充要条件是
=0成立的充要条件是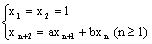 ,若T=1998是使得xT+1=xT+2=1的最小正整数,则
,若T=1998是使得xT+1=xT+2=1的最小正整数,则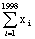 =___________.
=___________.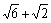 ),在平面的两侧各有一点S和T,满足SA=SB=SC=
),在平面的两侧各有一点S和T,满足SA=SB=SC=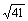 ,TA=TB=TC=5,则ST=___________.
,TA=TB=TC=5,则ST=___________.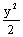 =1的右焦点作直线L交双曲线于A、B两点,若实数使得|AB|=的直线L恰有3条,则=_____________.
=1的右焦点作直线L交双曲线于A、B两点,若实数使得|AB|=的直线L恰有3条,则=_____________.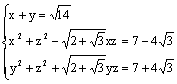 ,则z=_____________.
,则z=_____________.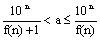 .
.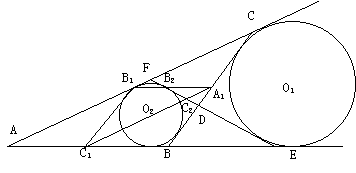 一、(50分)作两个不等圆⊙O1,⊙Q2的四条公切线,如图,点A为两外公切线的交点,点D为两内公切线的交点,点B,C,E,F是两类公切线的交点,记A1,B1,C1分别为BC,CA,AB的中点,若EF与A1B1交于B2,与A1C1交于C2,求证:B1,C1,C2,B2共圆.
一、(50分)作两个不等圆⊙O1,⊙Q2的四条公切线,如图,点A为两外公切线的交点,点D为两内公切线的交点,点B,C,E,F是两类公切线的交点,记A1,B1,C1分别为BC,CA,AB的中点,若EF与A1B1交于B2,与A1C1交于C2,求证:B1,C1,C2,B2共圆.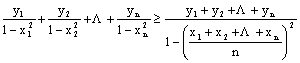
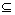 Sn,Y
Sn,Y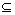 Sn(X,Y无顺序),若X
Sn(X,Y无顺序),若X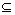 Y或Y
Y或Y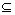 X,则称X,Y为一对包含子集对,否则称为非包含子集对,问Sn中是包含子集对多还是非包含子集对多?证明你的结论。
X,则称X,Y为一对包含子集对,否则称为非包含子集对,问Sn中是包含子集对多还是非包含子集对多?证明你的结论。