同余式与不定方程
同余式和不定方程是数论中古老而富有魅力的内容.考虑数学竞赛的需要,下面介绍有关的基本内容.
1. 同余式及其应用
定义:设a、b、m为整数(m>0),若a和b被m除得的余数相同,则称a和b对模m同余.记为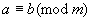 或
或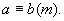
一切整数n可以按照某个自然数m作为除数的余数进行分类,即n=pm+r(r=0,1,,m-1),恰好m个数类.于是同余的概念可理解为,若对n1、n2,有n1=q1m+r,n2=q2m+r,那么n1、n2
对模m的同余,即它们用m除所得的余数相等.
利用整数的剩余类表示,可以证明同余式的下述简单性质:
(1) 若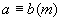 ,则m|(b-a).反过来,若m|(b-a),则
,则m|(b-a).反过来,若m|(b-a),则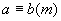 ;
;
(2) 如果a=km+b(k为整数),则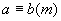 ;
;
(3) 每个整数恰与0,1,,m-1,这m个整数中的某一个对模m同余;
(4) 同余关系是一种等价关系:
① 反身性 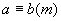 ;
;
② 对称性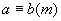 ,则
,则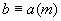 ,反之亦然.
,反之亦然.
③ 传递性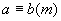 ,
,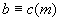 ,则
,则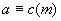 ;
;
(5)如果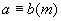 ,
,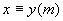 ,则
,则
①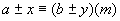 ;
;
②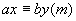 特别地
特别地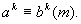
应用同余式的上述性质,可以解决许多有关整数的问题.
例1(1898年匈牙利奥林匹克竞赛题)求使2n+1能被3整除的一切自然数n.
解∵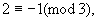
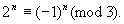
则2n+1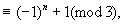
当n为奇数时,2n+1能被3整除;
当n为偶数时,2n+1不能被3整除.
例2 求2999最后两位数码.
解 考虑用100除2999所得的余数.
∵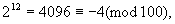
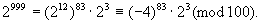
又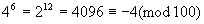
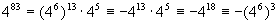
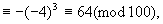
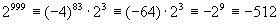
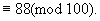
2999的最后两位数字为88.
例3 求证31980+41981能被5整除.
证明 ∵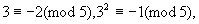
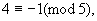
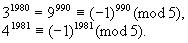
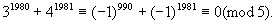
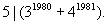
2.不定方程
不定方程的问题主要有两大类:判断不定方程有无整数解或解的个数;如果不定方程有整数解,采取正确的方法,求出全部整数解.
(1) 不定方程解的判定
如果方程的两端对同一个模m(常数)不同余,显然,这个方程必无整数解.而方程如有解则解必为奇数、偶数两种,因而可以在奇偶性分析的基础上应用同余概念判定方程有无整数解.
例4 证明方程2x2-5y2=7无整数解.
证明 ∵2x2=5y2+7,显然y为奇数.
① 若x为偶数,则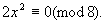
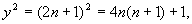
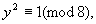
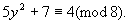
∵方程两边对同一整数8的余数不等,
x不能为偶数.
② 若x为奇数,则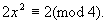
但5y2+7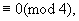
x不能为奇数.因则原方程无整数解.
说明:用整数的整除性来判定方程有无整数解,是我们解答这类问题的常用方法.
例5 (第14届美国数学邀请赛题)不存在整数x,y使方程
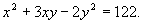 ①
①
证明 如果有整数x,y使方程①成立,
则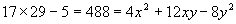
=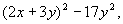 知(2x+3y2)+5能被17整除.
知(2x+3y2)+5能被17整除.
设2x+3y=17n+a,其中a是0,1,2,3,4,5,6,7,8中的某个数,但是这时(2x+3y)2+5=(17n)2+34na+(a2+5)=a2+5(mod17),而a2+5被17整除得的余数分别是5,6,9,14,4,13,7,3,1,即在任何情况下(2x+3y)2+5都不能被17整除,这与它能被17整除矛盾.故不存在整数x,y使①成立.
例7 (第33届美国数学竞赛题)满足方程x2+y2=x3的正整数对(x,y)的个数是( ).
(A)0 (B)1(C)2(D)无限个(E)上述结论都不对
解由x2+y2=x3得y2=x2(x-1),
所以只要x-1为自然数的平方,则方程必有正整数解.令x-1=k2(k为自然数),则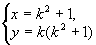 为方程的一组通解.由于自然数有无限多个,故满足方程的正整数对(x,y)有无限多个,应选(D).
为方程的一组通解.由于自然数有无限多个,故满足方程的正整数对(x,y)有无限多个,应选(D).
说明:可用写出方程的一组通解的方法,判定方程有无数个解.
(2) 不定方程的解法
不定方程没有统一的解法,常用的特殊方法有:配方法、因式(质因数)分解法、不等式法、奇偶分析法和余数分析法.对方程进行适当的变形,并正确应用整数的性质是解不定方程的基本思路.
例6 求方程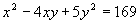 的整数解.
的整数解.
解(配方法)原方程配方得(x-2y)2+y2=132.
在勾股数中,最大的一个为13的只有一组即5,12,13,因此有8对整数的平方和等于132即(5,12),(12,5),(-5,-12),(-12,-5),(5-,12),(12,-5),(-5,12),(-12,5).故原方程组的解只能是下面的八个方程组的解
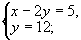
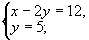
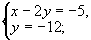
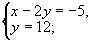
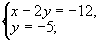
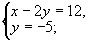
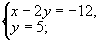
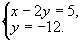
解得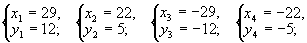
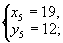
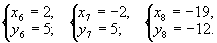
例7 (原民主德国1982年中学生竞赛题)已知两个自然数b和c及素数a满足方程a2+b2=c2.证明:这时有a<b及b+1=c.
证明(因式分解法)∵a2+b2=c2,
a2=(c-b)(c+b),
又∵a为素数,c-b=1,且c+b=a2.
于是得c=b+1及a2=b+c=2b+1<3b,
即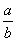 <
<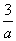 .而a3,
.而a3,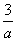 1,
1,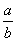 <1.a<b.
<1.a<b.
例9(第35届美国中学数学竞赛题)满足联立方程
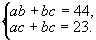
的正整数(a,b,c)的组数是( ).
(A)0 (B)1 (C)2 (D)3 (E)4
解(质因数分解法)由方程ac+bc=23得
(a+b)c=23=123.
∵a,b,c为正整数,c=1且a+b=23.将c和a=23-b代入方程ab+bc=44得
(23-b)b+b=44,即(b-2)(b-22)=0,
b1=2,b2=22.从而得a1=21,a2=1.故满足联立方程的正整数组(a,b,c)有两个,即(21,2,1)和(1,22,1),应选(C).
例10求不定方程2(x+y)=xy+7的整数解.
解 由(y-2)x=2y-7,得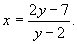
分离整数部分得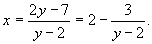
由x为整数知y-2是3的因数,
y-2=1,3,x=3,5,1.
方程整数解为
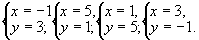
例11 求方程x+y=x2-xy+y2的整数解.
解(不等式法)方程有整数解 必须△=(y+1)2-4(y2-y)0,解得
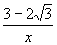
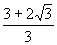 .
.
满足这个不等式的整数只有y=0,1,2.
当y=0时,由原方程可得x=0或x=1;当y=1时,由原方程可得x=2或0;当y=2时,由原方程可得x=1或2.
所以方程有整数解
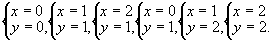
最后我们来看两个分式和根式不定方程的例子.
例12 求满足方程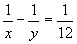 且使y是最大的正整数解(x,y).
且使y是最大的正整数解(x,y).
解将原方程变形得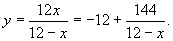
由此式可知,只有12-x是正的且最小时,y才能取大值.又12-x应是144的约数,所以,
12-x=1,x=11,这时y=132.
故 满足题设的方程的正整数解为
(x,y)=(11,132).
例13(第35届美国中学生数学竞赛题)满足0<x<y及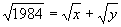 的不同的整数对(x,y)的个数是( ).
的不同的整数对(x,y)的个数是( ).
(A)0 (B)1 (C)3 (D)4 (E)7
解法1 根据题意知,0<x<1984,由
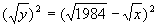
得 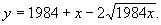
当且仅当1984x是完全平方数时,y是整数.而1984=2631,故当且仅当x具有31t2形式时,1984x是完全平方数.
∵x<1984,∵17.当t=1,2,3时,得整数对分别为(31,1519)、(124,1116)和(279,775).当t>3时yx不合题意,因此不同的整数对的个数是3,故应选(C).
解法2 ∵1984=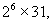
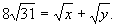 由此可知:x必须具有31t2形式,y必须具有31k2形式,并且t+k=8(t,k均为正整数).因为0<x<y,所以t<k.当t=1,k=7时得(31,1519);t=2,k=6时得(124,1116);当t=3,k=5时得(279,775).因此不同整数对的个数为3.
由此可知:x必须具有31t2形式,y必须具有31k2形式,并且t+k=8(t,k均为正整数).因为0<x<y,所以t<k.当t=1,k=7时得(31,1519);t=2,k=6时得(124,1116);当t=3,k=5时得(279,775).因此不同整数对的个数为3.
练习二十
1. 选择题
(1)方程x2-y2=105的正整数解有( ).
(A) 一组 (B)二组 (C)三组 (D)四组
(2)在0,1,2,,50这51个整数中,能同时被2,3,4整除的有( ).
(A) 3个 (B)4个 (C)5个 (D)6个
2.填空题
(1)的个位数分别为_________及_________.
(2)满足不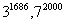 等式104105的整数A的个数是x104+1,则x的值________.
等式104105的整数A的个数是x104+1,则x的值________.
(3) 已知整数y被7除余数为5,那么y3被7除时余数为________.
(4) (全俄第14届中学生数学竞赛试题)求出任何一组满足方程x2-51y2=1的自然数解x和y_________.
3.(第26届国际数学竞赛预选题)求三个正整数x、y、z满足
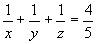 .
.
4.(1985年上海数学竞赛题)在数列4,8,17,77,97,106,125,238中相邻若干个数之和是3的倍数,而不是9的倍数的数组共有多少组?
5.求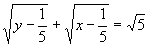 的整数解.
的整数解.
6.求证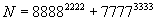 可被37整除.
可被37整除.
7.(全俄1986年数学竞赛题)求满足条件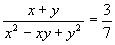 的整数x,y的所有可能的值.
的整数x,y的所有可能的值.
8.(1985年上海初中数学竞赛题)已知直角三角形的两直角边长分别为l厘米、m厘米,斜边长为n厘米,且l,m,n均为正整数,l为质数.证明:2(l+m+n)是完全平方数.
9.(1988年全国初中数学竞赛题)如果p、q、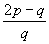 、
、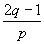 都是整数,并且p>1,q>1,试求p+q的值.
都是整数,并且p>1,q>1,试求p+q的值.
练习二十
1.D.C.
2.(1)9及1. (2)9. (3)4.
(4)原方程可变形为x2=(7y+1)2+2y(y-7),令y=7可得x=50.
3.不妨设xz,则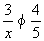 ,故x3.又有
,故x3.又有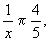 故x2.若x=2,则
故x2.若x=2,则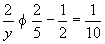 ,故y6.又有
,故y6.又有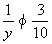 ,故y4.若y=4,则z=20.若y=5,则z=10.若y=6,则z无整数解.若x=3,类似可以确定34,y=3或4,z都不能是整数.
,故y4.若y=4,则z=20.若y=5,则z=10.若y=6,则z无整数解.若x=3,类似可以确定34,y=3或4,z都不能是整数.
4.可仿例2解.
5.先求出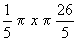 ,然后将方程变形为y=5+x-2
,然后将方程变形为y=5+x-2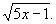 要使y为整数,5x-1应是完全平方数,,解得
要使y为整数,5x-1应是完全平方数,,解得
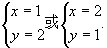
6.88888(mod37),8888222282(mod37).
77777(mod37),7777333373(mod37),88882222+77773333(82+73)(mod37),而82+73=407,37|407,37|N.
7.简解:原方程变形为3x2-(3y+7)x+3y2-7y=0由关于x的二次方程有解的条件△0及y为整数可得05,即y=0,1,2,3,4,5.逐一代入原方程可知,原方程仅有两组解(4,5)、(5,4).
8.∵l2+m2=n2,l2=(n+m)(n-m).∵l为质数,且n+m>n-m>0,n+m=l2,n-m=1.于是l2=n+m=(m+1)+m=2m+1,2m=l2-1,2(l+m+1)=2l+2+2m=l2+2l+1=(l+1)2.即2(l+m+1)是完全平方数.
9.易知pq,不妨设p>q.令 =n,则m>n由此可得不定方程(4-mn)p=m+2,解此方程可得p、q之值.
=n,则m>n由此可得不定方程(4-mn)p=m+2,解此方程可得p、q之值.
- 2013年南开大学录取分数线
- 2013年内蒙古大学录取分数线
- 北京服装学院2013高考在京二本提档分数线
- 2013年北京大学录取分数线
- 2013年内蒙古农业大学录取分数线
- 2013年浙江大学录取分数线
- 天津大学在天津录取780人 理科最低分613
- 2013年湖南师范大学录取分数线
- 河北工业大学2013年录取分数线
- 2013年北京师范大学录取分数线
- 北方工业大学2013高考在京二本录取分数线
- 2013年华中师范大学录取分数线
- 北京工商大学2013高考二本在京录取分线线
- 首都师范大学2013高考在京二本分数线:文531 理538
- 2013年辽宁大学录取分数线
- 2013年中国传媒大学录取分数线
- 2013年福建工程学院录取分数线
- 北京信息科技大学2013高考在京二本录取分数线
- 2013年清华大学录取分数线
- 2013年中国矿业大学录取分数线
- 2013年西安交通大学录取分数线
- 北京石油化工学院2013高考在京二本分数线
- 2013年哈尔滨工业大学录取分数线
- 国防科技大学2013年高考录取分数线统计
- 2013年大连海事大学录取分数线