1999年河北省高中数学竞赛试题
| 1999年河北省高中数学竞赛试题 |
|
班级 姓名 一、选择题 1、已知logab+3logba= A、13 B、4 C、2 D、1 2、设M={a|a= A、10个 B、64个 C、128个 D、256个 3、将边BC=15cm的ABC绕边AC旋转一周,所得旋转体是有公共底面的两个圆锥,边AB形成的圆锥的侧面展开图是半径为20cm,圆心角为2160的扇形,则此旋转体内切球的半径是 ( ) A、 4、设x2+3y2-4x+6y+3 A、[3,7] B、[1,9] C、[3- 5、x+y+z=1999的正整数解的个数是 ( ) A、9981997 B、9991997 C、9991999 D、10001999 6、一个正方体内接于一个圆锥(其中一个底面在圆锥底面上,相对的面的四个顶点均在圆锥的侧面上),经过圆锥的两条母线作截面,则下列图形中不可能出现的图形个数是 ( ) A、5 B、4 C、3 D、2
二、填空题(每小题9分) 7、 8、设三棱锥PABC中,PC 9、已知函数 10、若复数z满足|z+1+i|+|z-1-i|=2 11、设ap0,若方程x+logax=m的解为p,则方程x+ax=m的解是 ; 12、从6名男运动员中选4人,5名女运动员中选3人,分成3个小组去参加三个不同城市的体育比赛,要求每组中男运动员和女运动员至少各有1人,则不同的选派方案种数为 。(用数字作答) 三、解答题 13、(本题20分)设点P是双曲线 14、(本题20分)锐角 15、(本题20分)证明:x是任意实数时,使等式f(x+1)-2f(x)+f(x-1)=0成立的非常值函数f(x)=anxn+an-1xn-1++a1x+a0(an |
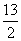 ,当a1时,
,当a1时,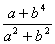 的值是( )
的值是( )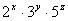 ,x,y,z均为非负整数}的子集为N={b|b
,x,y,z均为非负整数}的子集为N={b|b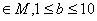 },则N的子集中包含元素1和10的集合有 ( )
},则N的子集中包含元素1和10的集合有 ( ) 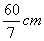 B、
B、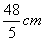 C、
C、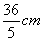 D、60cm
D、60cm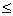 0,则x-3y的范围是( )
0,则x-3y的范围是( )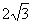 ,7+
,7+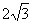 ] D、(5-
] D、(5-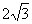 ,7)
,7)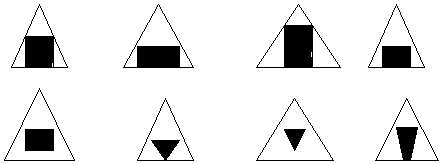
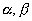 是x2+2px+1=0的两个虚根,若复平面上
是x2+2px+1=0的两个虚根,若复平面上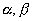 ,1对应的点构成正三角形,那么实数P= ;
,1对应的点构成正三角形,那么实数P= ;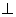 平面ABC,PC=AB=
平面ABC,PC=AB=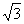 ,AC=
,AC=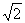 ,
,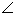 C为锐角,K为棱AB上的动点,则
C为锐角,K为棱AB上的动点,则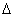 PCK面积的最小值为 ;
PCK面积的最小值为 ;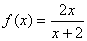 ,当x1=1,xn=f(xn-1)(n
,当x1=1,xn=f(xn-1)(n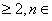 N)时,x1999= ;
N)时,x1999= ;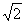 ,记|z+i|的最大值和最小值分别为M,m,则
,记|z+i|的最大值和最小值分别为M,m,则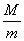 = ;
= ;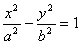 上除顶点外的任意一点,F1,F2分别为左、右焦点,c 为半焦距,
上除顶点外的任意一点,F1,F2分别为左、右焦点,c 为半焦距,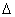 PF1F2的内切圆与边F1F2切于点M,求|F1M||F2M|的值。
PF1F2的内切圆与边F1F2切于点M,求|F1M||F2M|的值。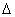 ABC的外心为O,O到三角形三边距离分别为
ABC的外心为O,O到三角形三边距离分别为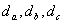 ,如果三角形外接圆半径为2,求
,如果三角形外接圆半径为2,求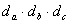 的最大值及最大值存在的条件。
的最大值及最大值存在的条件。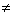 0)都能且只能表示成一次函数f(x)=ax+b(an
0)都能且只能表示成一次函数f(x)=ax+b(an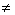 0)的形式。
0)的形式。