2002年宁波市高二数学竞赛(第一试)
| 2002年宁波市高二数学竞赛(第一试) |
|
(2002年3月23日上午8:30-10:00) 一、选择题(本题满分60分,每小题6分) 1.若实数集M={2a,a2-a},则a的取值范围是 ( ) (A) R (B) {a|a0,aR} (C) {a|a3,aR} (D) {a|a0且a3,aR} 2.满足 (A) 2499 (B) 2500 (C) 2501 (D) 10000 3.过点 (A) 0 (B) 无穷多 (C) 至少两条 (D) 只有一条 4.椭圆 (A) 5.函数f(x)是定义在R上的奇函数,且f(1-x)=f(1+x)恒成立,那么f(2002)=( ) (A) 1 (B) 2002 (C) 0 (D) 不能确定 6.设 (A) abc (B) bac (C) acb (D) cba 7.平行于棱锥底面的两个平面将锥体体积三等分,从锥顶向锥底的方向上锥高被分成的三部分的比是 ( ) (A) 3:2:1 (B) 8.用一个平面去截一个n棱柱(n3,nN),截去一个三棱锥,剩下的多面体顶点的数目是 (A) 2n-1,2n+1 (B) 2n-1,2n,2n+1,2n+2 (C) 2n-1,2n+1,2n+2 (D) 2n+1,2n+2 9.曲线 (A) 10.设等差数列{an}满足3a 8=5a13,且a10,Sn为其前n项之和,则Sn(nN)中最大的是 (A) S10 (B) S11 (C) S20 (D) S21 二、填空题(本题满分90分,每小题6分) 11.关于x的不等式a x2-2002x+b0的解集为(-3,-1),那么不等式bx2+2002x+a0的解集为 . 12.已知是第三象限角,6sin2+sincos-2cos2,则sin2+cos2的值是 . 13.关于x的方程2x2-4x+a-1=0至少有一个正实数根,则a的取值范围是 . 14.与x轴平行的直线l与双曲线 15.一张20012002的方格纸,设一条直线l穿过的方格数为k,则k的最大值为 . 16.正数x,y满足 17.已知函数 18.正方体ABCD-A1B1C1D1中,BD1与平面ACD1所成的角为 . 19.某商品计划减价,现有四种方案,方案①先减价m%。再减价n%;方案②先减价n%,再减价m%;方案③分两次减价,每次减价 已知m0,那么四种方案中,方案 减价最少。 20.方程sin4x+cos4x-sin2x+k0恒成立,则实数k的取值范围是 . 21.数2x,1,y-1成等差数列,并且y+3,|x+1|+|x-1|,cos(arccosx)成等比数列,则x+y+xy= . 22.已知函数y=||x-2|-a|的图象与直线y=3恰好有3个交点,则这三个交点的坐标为 . 23.使 24.已知数列{an}的前n项之和Sn=n2,记 则 25.定点P(a,0),Q是抛物线y2=4x上任一点,则|PQ|的最小值为 . |
- 军训口号大集结
- 盘点新生军训的9大注意事项
- 2011年高一同学军训心得体会
- 军训通讯稿 200字(1)
- 2011年新高一军训该注意些什么
- 高一新生军训:40多人一个班倒下10多个
- 军训自我鉴定范文 400字
- 军训总结:大学篇
- 军训个人总结 1000字
- 高一新生军训感想:有苦亦有乐
- 高一学生军训心得:回忆竟是如此美好
- 大学军训心得体会800字
- 大学军训心得体会1000字
- 军训心得体会 自我鉴定 总结大全
- 2011年高一军训心得体会1000字
- 2011年高一军训感想:你们让我幸福的事
- 北京高中军训样式多年不改 家长盼增新内容
- 军训带什么之:初中军训必备物品
- 军训日记:八百里分麾下炙,五十弦翻塞外声
- 小贴士:高中军训小提醒
- 初中军训心得体会:军训的泪水1000字
- 2011级新高一同学军训心得体会汇总
- 高一同学军训心得:让军训来涤荡我们的意志
- 范文指导:2011年高一军训感言1000字
- 难忘那一张笑脸——新高一学生潮汐夜影的军训实录
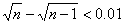 的最小正整数n是 ( )
的最小正整数n是 ( )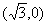 的所有直线中,通过两个不同有理点的直线的条数是 ( )
的所有直线中,通过两个不同有理点的直线的条数是 ( )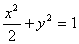 的两个焦点为F1,F2,过右焦点F2作倾角为
的两个焦点为F1,F2,过右焦点F2作倾角为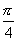 的弦AB,则△ABF1的面积为 ( )
的弦AB,则△ABF1的面积为 ( )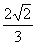 (B)
(B) 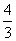 (C)
(C) 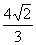 (D)
(D) 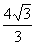
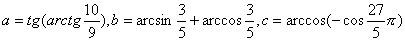 ,则 ( )
,则 ( )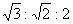 (C)
(C) 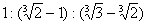 (D)
(D) 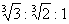
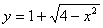 与直线
与直线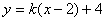 有两个不同的交点时,实数
有两个不同的交点时,实数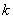 的取值范围是 ( )
的取值范围是 ( )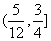 (B)
(B) 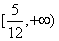 (C)
(C) 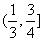 (D)
(D) 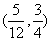
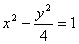 相交于M、N两点,又与它的渐近线交于E、F两点,E、F三等分线段MN,那么l与x轴的距离为 .
相交于M、N两点,又与它的渐近线交于E、F两点,E、F三等分线段MN,那么l与x轴的距离为 .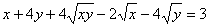 ,那么
,那么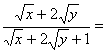 .
.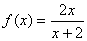 ,当
,当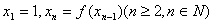 时,x2002= .
时,x2002= .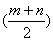 %;方案④一次性减价(m+n)%。
%;方案④一次性减价(m+n)%。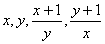 均为正整数的(x,y)共有 组.
均为正整数的(x,y)共有 组.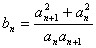 ,
,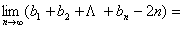 .
.