2000年全国高中数学联赛试题
一、 选择题(本题满分36分,每小题6分)
1.设全集是实数,若A={x|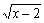 0},B={x|
0},B={x|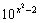 =
=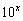 },则
},则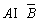 是( )
是( )
(A){2} (B){-1} (C){x|x2} (D)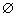
2.设sina>0,cosa<0,且sin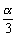 >cos
>cos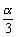 ,则
,则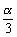 的取值范围是( )
的取值范围是( )
(A)(2kp+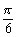 ,2kp+
,2kp+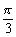 ), kZ (B)(
), kZ (B)(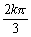 +
+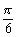 ,
,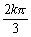 +
+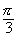 ),kZ
),kZ
(C)(2kp+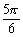 ,2kp+p),kZ(D)(2kp+
,2kp+p),kZ(D)(2kp+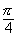 ,2kp+
,2kp+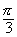 )
)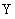 (2kp+
(2kp+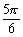 ,2kp+p),kZ
,2kp+p),kZ
3.已知点A为双曲线x2-y2=1的左顶点,点B和点C在双曲线的右分支上,△ABC是等边三角形,则△ABC的面积是( )
(A)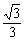 (B)
(B)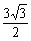 (C)3
(C)3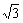 (D)6
(D)6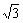
4.给定正数p,q,a,b,c,其中pq,若p,a,q是等比数列,p,b,c,q是等差数列,则一元二次方程bx2-2ax+c=0( )
(A)无实根 (B)有两个相等实根 (C)有两个同号相异实根 (D)有两个异号实根
5.平面上整点(纵、横坐标都是整数的点)到直线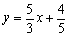 的距离中的最小值是( )
的距离中的最小值是( )
(A)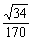 (B)
(B)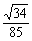 (C)
(C)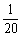 (D)
(D)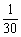
6.设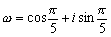 ,则以w,w3,w7,w9为根的方程是( )
,则以w,w3,w7,w9为根的方程是( )
(A)x4+x3+x2+x+1=0 (B) x4-x3+x2-x+1=0
(C) x4-x3-x2+x+1=0 (D) x4+x3+x2-x-1=0
二、填空题(本题满分54分,每小题9分)
7.arcsin(sin2000)=__________.
8.设an是(3-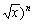 的展开式中x项的系数(n=2,3,4,),则
的展开式中x项的系数(n=2,3,4,),则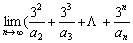 )=________.
)=________.
9.等比数列a+log23,a+log43,a+log83的公比是____________.
10.在椭圆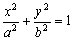 (a>b>0)中,记左焦点为F,右顶点为A,短轴上方的端点为B.若该椭圆的离心率是
(a>b>0)中,记左焦点为F,右顶点为A,短轴上方的端点为B.若该椭圆的离心率是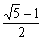 ,则ABF=_________.
,则ABF=_________.
11.一个球与正四面体的六条棱都相切,若正四面体的棱长为a,则这个球的体积是________.
12.如果:(1)a,b,c,d都属于{1,2,3,4};(2)ab,bc,cd,da;(3)a是a,b,c,d中的最小值,那么,可以组成的不同的四位数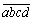 的个数是_________.
的个数是_________.
三、解答题(本题满分60分,每小题20分)
13.设Sn=1+2+3++n,nN,求f(n)=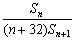 的最大值.
的最大值.
14.若函数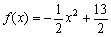 在区间[a,b]上的最小值为2a,最大值为2b,求[a,b].
在区间[a,b]上的最小值为2a,最大值为2b,求[a,b].
15.已知C0:x2+y2=1和C1: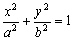 (a>b>0)。试问:当且仅当a,b满足什么条件时,对C1上任意一点P,均存在以P为项点,与C0外切,与C1内接的平行四边形?并证明你的结论。
(a>b>0)。试问:当且仅当a,b满足什么条件时,对C1上任意一点P,均存在以P为项点,与C0外切,与C1内接的平行四边形?并证明你的结论。
【加试】(10月15日上午10∶00-12∶00)
一.(本题满分50分)
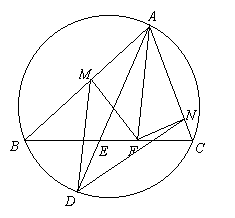 如图,在锐角三角形ABC的BC边上有两点E、F,满足BAE=CAF,作FMAB,FNAC(M、N是垂足),延长AE交三角形ABC的外接圆于D.证明:四边形AMDN与三角形ABC的面积相等.
如图,在锐角三角形ABC的BC边上有两点E、F,满足BAE=CAF,作FMAB,FNAC(M、N是垂足),延长AE交三角形ABC的外接圆于D.证明:四边形AMDN与三角形ABC的面积相等.
二.(本题满分50分)
设数列{a n}和{b n }满足,且
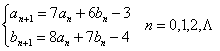
证明a n(n=0,1,2,)是完全平方数.
三.(本题满分50分)
有n个人,已知他们中的任意两人至多通电话一次,他们中的任意n-2个人之间通电话的次数相等,都是3 k次,其中k是自然数,求n的所有可能值.
- 复旦大学录取通知书附上手绘“校园生活指南”
- 清华大学2013高考计划招收本科生3372人
- 北工大校长亲自为48名新生颁录取通知书
- 清华不承认四川高考加分 是大学自主权的体现
- 北京大学2013年在山西计划招生78人 同比去年增23人
- 首都医科大学2013级新生入学须知
- 美女毕业照刷爆人大官网 质疑招生走美女路线
- 北京中医药大学2013年新生入学指南
- “上清华不拼爹”要追求普遍性公平
- 南开大学:2013年6个专业按大类招生
- 《上大学网第二批中国虚假大学警示榜(共50所)》榜单简介
- 原重庆大学校长林建华任浙大校长
- 大学招生变口味:传统文科专业示好理科生
- 北大清华高招忙“掐尖” 姊妹花携手奔清华
- 哈尔滨工业大学2013年本科新生入学须知
- 高校轻文重理现象严重 理科生考本科更易
- 首批赴台大陆学生遇就业困惑:毕业不能留台工作
- 北大招办主任秦春华:坚守教育工作者的良知 责任和诚信
- 高职校部分热门专业受追捧 录取线超三本
- 第二批虚假大学警示榜发布 假大学紧盯落榜生
- 招生考试院支招辨别高校录取通知书真伪
- 北京交通大学2013级本科新生入学安排
- 2013北京高考一志愿报清华还有机会改专业
- 北大录取2761人 自主招生考生20%为农村户籍
- 北京工业大学2013级新生入学须知
- 中南财政政法大学2013年在海南计划招100人
- 厦门理工学院增新专业 烤面包也能拿本科学历
- 清华大学2013级学生入学教育及军训政训时间安排
- 高招大小年现象抬头 名校投档线波动几百位
- 中科院院士:反对“一二三本”大学提法 五年内或取消