平面图形的面积
1. 关于面积的两点重要知识
(1)相似三角形的面积比等于相似比的平方
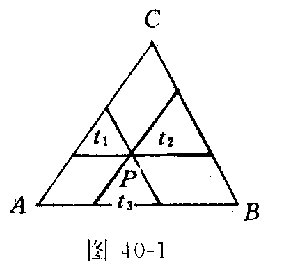
例1(第2届美国数学邀请赛题)如图40-1,在△ABC的内部选取一点P,过P点作三条分别与△ABC的三条边平行的直线,这样所得的三个三角形t1、t2和t3的面积分别为4,9和49.求△ABC的面积.
解 设T是△ABC的面积,T1、T2和T3分别是三角形t1、t2和t3的面积;c是边AB的长,c1、c2和c3分别是平行于边AB的三个三角形t1、t2和t3的边长.那么,由四个三角形相似,得
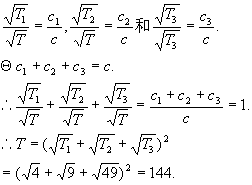
(2)两边夹角的三角形面积,灵活运用△ABC的面积公式S=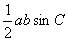 可以方便地解决一些较难的面积问题.
可以方便地解决一些较难的面积问题.
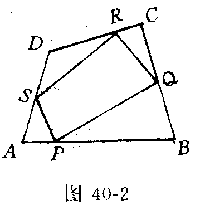
例2已知P、Q、R、S四点分别由四边形的四个顶点A、B、C、D同时开始沿四边形各边依反时针方向以各自的速度作匀速直线运动(如图40-2),已知P由A至B,R由C至D分别需要两秒钟;Q由B至C,S由D至A分别需要1秒钟;问开始运动后,经过多少时间,四边形PQRS的面积最小?
解设P的速度是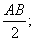 Q的速度是
Q的速度是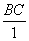 ;R的速度是
;R的速度是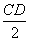 ,S的速度是
,S的速度是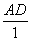 .在t(0<t1)秒时,AP=
.在t(0<t1)秒时,AP=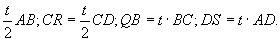
设四边形PQRS和四边形ABCD的面积分别为S、S.
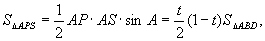 ①
①
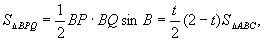 ②
②
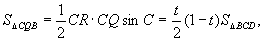 ③
③
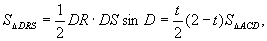 ④
④
①+③得,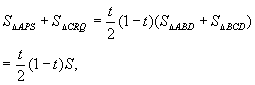
②+④得,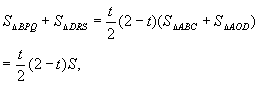
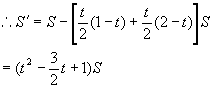
当t= 有极小值.
有极小值.
答:经过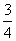 秒后,四边形PQRS面积最小.
秒后,四边形PQRS面积最小.
下面是一个用不等式来证明相等问题的例子.
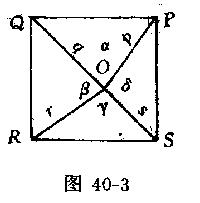
例3(1982年英国数学奥林匹克竞赛试题).PQRS是面积为A的四边形.O是在它内部的一点,证明:如果2A=OP2+OQ2+OR2+OS2
那么PQRS是正方形并且O是它的中心.
证明 如图40-3,按题设有 此处无图
p2+q2+r2+s2=pqsin+qrsin+rsin+spsin
pq+qr+rs+sp ①
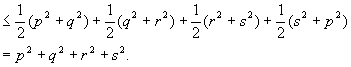
依题设、必须且只须这里所有的不等式都取等号.由①取等号有
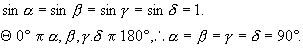
由②取等号有p=q=r=s
因此PQRS是正方形,O是它的中心.
2.等积变换与面积法
等积变换的特点是利用图形之间的面积相等或成比例的转换来解题.
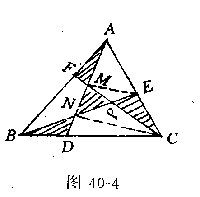
例4(第17届苏联竞赛题)图40-4中阴影所示的四个三角形面积相等.求证:无阴影所示的四个三角形面积相等.求证:无阴影的三个四边形的面积也相等.
证明 如图:连ME、NC.
∵S△NME=S△CEM,
ME∥NC.
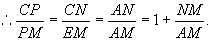
若设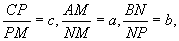 则由上式可得
则由上式可得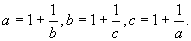 解以上三式的联立方程组可得
解以上三式的联立方程组可得
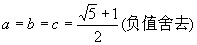 .
.
这样,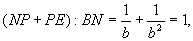 则N为BE中点.
则N为BE中点.
又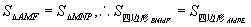
同理可证 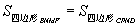
例5(第9届全俄中学竞赛题)如图40-5在凸五边形ABCDE中,对角线CE分别交对角线BD、AD于F、G,BF:FD=5:4,AG:GD=1:1,CF:FG:GE=2:2:3,求△CFD和△ABE的面积比.
解 连AF.∵CF:FG:GE=2:2:3,
S△CFD:S△DFG:S△DEG=2:2:3.
S△CFD=S,则S△FDG=S,S△DGF=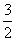 S.
S.
又BF:FD=5:4,S△BEF:S△FDE=5:4.
S△BEF=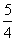 (S△FDG+S△DEG)=
(S△FDG+S△DEG)=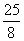 S
S
又由BF:FD=5:4,S△ABF:S△AFD=5:4.
S△ABE=SABFE-S△BFE
=(S△ABF+S△AFG+S△AGE)-S△BFE
=5S-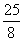 S=
S=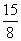 S
S
(∵AG:GD=1:1).
即S△CFD:S△ABE=8:15.
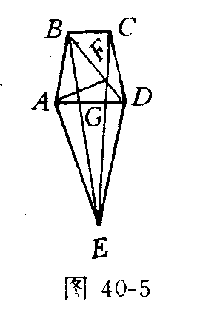
例6 六边形ABCDEF内接于⊙O,且AB=BC=CD=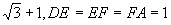 (如图40-6(a)),求此六边形的面积.
(如图40-6(a)),求此六边形的面积.
分析 如果连OA、OB、OC、OD、OE、OF,那么容易看出
S△AOB=S△BOC=S△COD,
S△DOE=S△EOF=S△FOA.
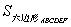 =S△AOB+S△BOC+S△COD+S△DOE+S△EOF+S△FOA.
=S△AOB+S△BOC+S△COD+S△DOE+S△EOF+S△FOA.
从加法满足交换律联想到图形可以改变位置而重新组合,于是把已知六边形改成等积的新的六边形ABCDEF,其中,⊙O与⊙O为等圆,且AF=BC=DE=1,AB=CD=EF=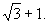 把AB,CD,EF分别向两方延长得交点M、N、P(如图40-6(b)),容易证明BAF=120等,从而△MNP为等边三角形.
把AB,CD,EF分别向两方延长得交点M、N、P(如图40-6(b)),容易证明BAF=120等,从而△MNP为等边三角形.
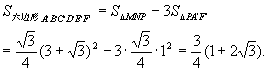
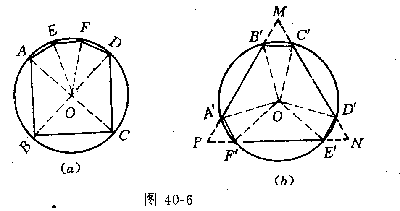
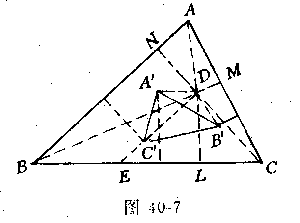
例7(1962年上海竞赛题)已知△ABC∽△ABC如图40-7,AB=c,BC=a,CA=b,A、B、C到BC、CA、AB的距离分别为l、m、n.求证:la+mb+nc=2S△ABC.
分析 欲证上述结论,只须证S△ABC+S△BCA+S△CAB=S△ABC.
我们试想,当△ABC收缩为一点时,上式显然成立,因此,如果我们能够做到在将△ABC逐渐收缩为一点的过程中,保持左边三项的面积始终不变,那么问题便解决了.为了保持△ABC面积不变,我们试用等积工具,设法使A沿平行于BC的直线运动,同样B、C分别沿着平行于CA、AB的直线运动.而这三条分别平行于BC、CA、AB的直线如能共点,即反映△ABC可收缩为一点.
证明 分别过B,C作直线BD∥CA,CD∥BA,直线CD交BD于D、交BC于E.
则CDB=BAC,又△ABC∽△ABC,
△BAC=BAC=CDB.这说明C、D、A、B四点共圆,ADC=ABC=ABC=DEC,AD∥BC.
过D分别作DLBC于L,DMCA于M,DNAB于N,连DA、DB、DC、则由DA∥BC、DB∥CA,DC∥AB,得DL=l,DM=m,DN=n.
于是la+mb+nc=DLBC+DMAC+DNAB=2(S△DBC+S△DCA+S△DAB)=2S△ABC.
有些看似与面积无关的几何问题,如能够巧妙地引入面积关系,便可迅速求解,这就是所谓的面积法.
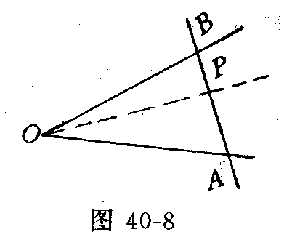
例8(美国数学竞赛题)在一个给定的角O内,任决地给定一点P,过P作一直线交定角的两边于A、B两点(如图40-8),问过P作怎样的直线才能使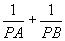 最大?
最大?
解设OPB=,△OPA、△OPB的面积分别为S1、S2,则
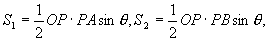
于是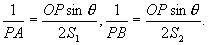
因此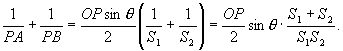
但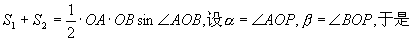
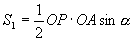 ,
,
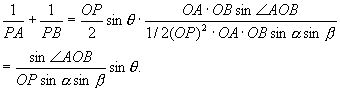
当=90时,sin取得最大值1,因此当过P点的直线与OP垂直时,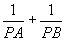 达到最大值
达到最大值
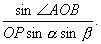
3. 杂题
竞赛中出现的一些综合性较强的面积问题,一般采用简化图形或根据题意构造适当的图形来处理.
例9(1987年全俄中学生竞赛题)凸四边形ABCD的面积为S.K、L、M、N分别是AC、AD、BC和BD的中点.证明:SKLNM<0.5S.
证明 设P、Q分别是AB、CD的中点(如图40-9).注意到PLQM、MKNL都是平行四边形,且SKLNM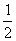 =S,因此,只须证明KLNM含于PLQM内.
=S,因此,只须证明KLNM含于PLQM内.
设PL、MQ分别交AC于E、F,则点K位于E、F之间.若不然,例如点K在线段AE上,则有AKAE,因EF=PM=AK=0.5AC,故有关系式AC=2AK=AK+EFAE+EF<AC,矛盾.同理K也不能在F.C之间,于是K在PLQM内.同样可证N也在PLQM内,由此得SKLNM<SPLQM=0.5S.
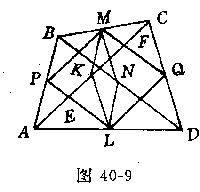
例10(第20届全苏中学生竞赛题)M点在锐角△ABC的AC边上,作△ABM和△CBM的外接圆.问当M点在什么地方时,两外接圆公共部分的面积最小?
解 设O、O1分别是△ABM和△CBM外接圆的圆心.两外接圆的公共部分面积是两个以BM为公共弦的弓形面积之和,可以考虑保时弓形的面积最小.
注意到
BOM=2BAM=常数.
BO1M=2BCM=常数.
因此,研究当弓形所对的圆心角固定时,弓形面积与弓形弦的关系.设圆心角为,弓形弦长为b,那么弓形的面积为
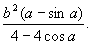
由此可见,上图中若BM越小,则每个弓形的面积越小、所以当BM是△ABC的高,即BMAC,M为垂足时,两外接圆公共部分的面积最小.
例11 设A、B为半径等于1的⊙O上任意两点,若过A、B的任意线段或曲线段L将⊙O面积平分,则L的长l必不小于2.
证明 若AB为⊙O的直径,且L为直线时,显然L将⊙O面积平分,这时l=2.
若AB是⊙O的直径,L不是直线时,则l>AB,即l>2.
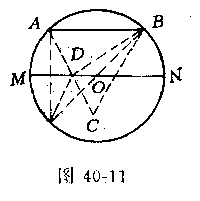
若AB不是⊙O的直径,如图40-11,作平行于AB的直径MN,作A关于MN的对称点A,A必在⊙O上,连AB,易知AB为⊙O的直径.由曲线L平分⊙O知,L上必有点与A、B在MN的异侧.取这样的一点C,并连结AC、BC,AC交MN于D,连BD、AD,则
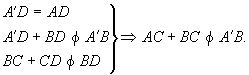
据此易证lAC+BC>2.
综上得l2,即L的长必不小于2.
最后我们介绍解决三角形面积问题的一个重要技巧三角形的剖分.将任意△ABC的三边BC、CA、AB分别分成n等分,然后过这些分点作平行于其他两边的直线,这样将△ABC分成若干个全等的小三角形(如图40-12)的手续,叫做对△ABC进行剖分.究竟分成多少等分,则视需要而定.
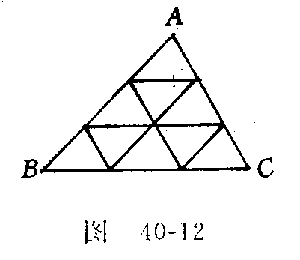
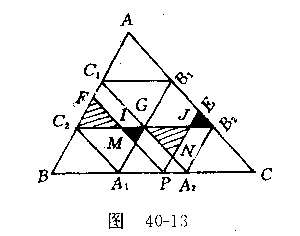
例12(1984年全国数学竞赛题)P为△ABC的边BC上任一点,作PE∥AB,PF∥AC.设△ABC的面积等于1.求证:△BPF、△PCE、四边形AFPE的面积中,至少有一个不小于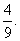
证明 如图40-13,作△ABC的剖分.这时每一个小三角形的面积均等于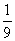 .
.
显然,如果点P在线段BA1上变动时,△PCE完整地盖住了四个小三角形,因此△PCE的面积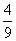 .对称地,如果点P落在线段A2C上,则△BPF的面积
.对称地,如果点P落在线段A2C上,则△BPF的面积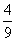 .
.
余下的只须讨论点P在线段A1A2内变动的情形,利用平行线的基本性质可证.
△FC2I≌△MA1P≌△NJG.
这说明上图中带阴影的两个三角形有相等的面积.又因为
△ EJ2B≌△NPA2≌△MGI,
这说明图中涂黑了的两个三角形面积相等.
将四边形AFPE中△NJG剪下来再拼到△FC2I上;把△MGI剪下来再拼到△EB2J2上,我们看出:
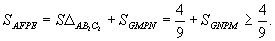
- 高三孩子早恋 家长该如何处理?
- 高三生处于备考“瓶颈期” 学不进去怎么办
- 高三家长陪考手记:用恰当的方式爱孩子
- 访谈实录:北京文科状元、理科榜眼做客搜狐网(2)
- 高考状元学习成功锦囊
- 高考关键阶段家长如何帮孩子调节压力
- 不同状态考生的考前安抚
- 真实案例:高三妈妈全心为孩子却被厌烦
- 孩子考试总答不完卷怎么破?
- 访谈实录:北京文科状元、理科榜眼做客搜狐网(一)
- 高考关键期如何调整好状态?
- 考前两月如何帮高三生逆袭
- 高考填报志愿家长和考生容易陷入的四大误区
- 专家支招:良好睡眠是最佳营养剂
- 安徽理科状元 机会只偏爱有准备的头脑
- 高考后放松 打游戏喝酒K歌一定要适度
- 2005高考状元全国巡回讲座内容实录(2)
- 高考二模考试过后 调整心态最关键
- 清华学子母亲日记:超常儿子的平常生活
- 13位2005年高考状元英语学习经验集锦
- 2005高考状元全国巡回讲座内容实录
- 高三家长的8种焦虑表现 拒绝情绪传染
- 四大高考状元这样冲刺
- 高考家长如何约法三章成功帮孩子戒掉恶习?
- 高考状元自述:我的一天